作者：MEWS矩阵

全文2117字，欢迎关注！

美国医生在各州分布的不等性以及且医生的供需及服务之间的影响一直是经济学家与健康政策管理者中的热门话题。如果医生们选择就近工作等与需求无关的原因，同时，如果在确定了工作地点后，医生们可以提升或降低病人对他们服务的需求，这种需求独立于医疗服务价格之外，这种假设在经济学和公共政策下的影响已经被发现了。许多医生相信他们有接近无限的力量去改变市场需求，这种观点来自于他们的自我评价，治疗经历以及医疗服务与效用之间的相关性，但是怀疑论者同样提供了一些关于相关性的其他解释。这篇文章的目的是为了就这个问题通过多方程、多变量的分析来分析在美国不同地区的外科医生和手术的供需之间的差异。

需求变化假设

标准经济学分析假设了供给与需求在任何市场下都是独立的。而需求变化假设则是指，当医生的外部供给发生变化的时候，对医生的外部需求也会发生一个变化，如下图：

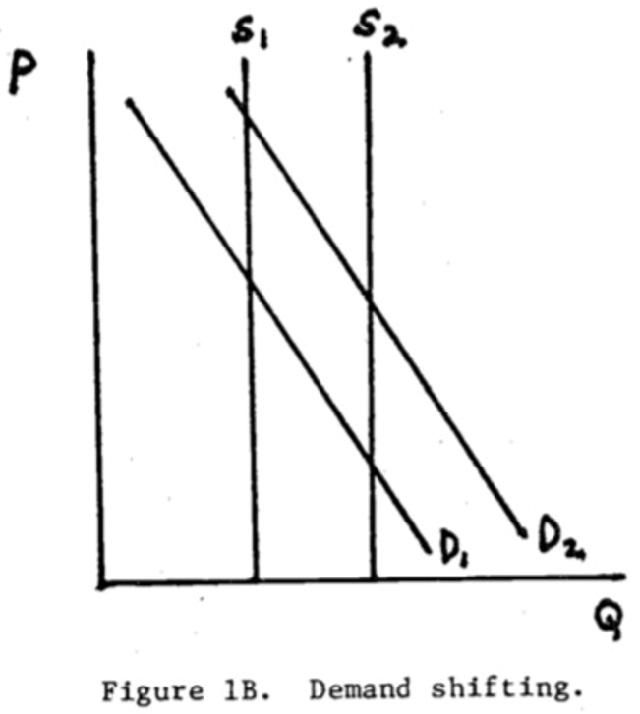
分析方法与基础数据

这篇文章的分析方法是建立一个需求方程，其中包括一些常见的用于确定需求的变量（如人口分布特征，收入，手术价格），再加上被预测好的医生的供给变量。预测的医生供给时通过用外科医生/人口的比率和一些其他用于确定医生位置的变量建立的回归方程来预测得到的。通过1963年和1970年的数据，作者建立了截面回归方程，同时美国健康采访调查机构（HIS）提供了22个洲的效用数据。其他回归方程则是用了HIS提供的更详细的数据，其中作者会根据个体的年龄，性别，人种，教育水平以及居住地来交叉定义。通过这些变量建立的回归更能保证对于人口结构变化的控制以及测试Pauly关于“需求变化对部分人群更加重要“的论点。

关于其他数据的获得部分，效用数据是通过HIS提供的数据计算得到，医生的供给数据来自于美国AMA关于医生分布的数据。另外一些数据主要来源于人口局与劳动力统计局。根据这些数据来源，作者总结如下：

内生数据：

Q：每十万人中手术操作的数量

S：每十万人中外科手术专家的数量

METS：该变量仅用于非市区，在市区中该变量为0.该变量是给予对市区外科医生数量/总人口的预测。

外生数据：

INC：每个单位个体的收入水平

HOTEL：旅馆与汽车旅馆的单人价位

NOMET：用于非市区的哑变量

NRMET：非市区人口在国家的分数。当该变量应用于市区地区的时候为0

%WYTE：白种人的比例

GP*：每十万人中从业人员的数量

回归结果

下表展示了应用以上变量得出的外科医生的位置的回归结果，回归结果是非常拟合的（R^2=0.96，代表96%的数据可以被解释）且参数对具体数据的变化并不敏感。NOMET参数是非常显著的并且接近-25，而NRMET的参数接近14. 这表明了在每十万人中，市区的外科医生数量要比非市区的外科医生数量平均多14人。HOTEL代表了人对不同地区到访和度假的程度。%WYTE是正值且非常显著，至于GP变量并不显著。

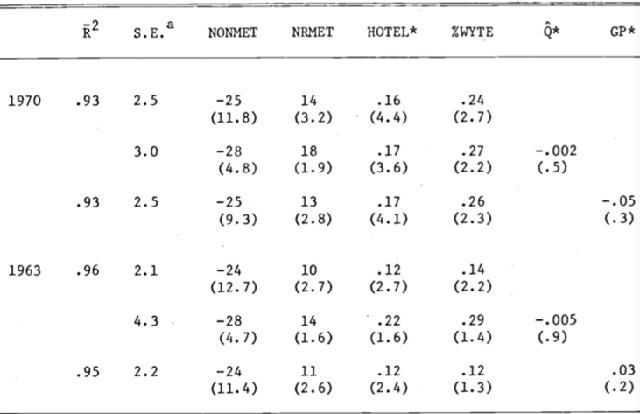
下表反映了在美国22个地区中需求回归的结果。总体来说，结果支持了外部供给的变化会改变外部需求的观点。在单位区域中每增加一个医生，每年将会增加40到60台手术。而外科医生的数量则可以通过S在HOTEL，%WYTE和%MET上预测出来，整体结果较为显著（R^2=0.8）。而收入方面，收入变量在需求方程中恒为正值，但是在预测外科医生供给上并不显著。

下图展示了关于需求方面的回归。回归的主要系数是预测的手术医生数量。METS*这个用于测量不同市区地区差异性的变量在这里并没有很显著的效果。而唯一一个可以在市区地区回归分析中保持显著的变量是GP*。总的来说这种分开的回归方程有利的支持了需求变化的假设并且反驳了市区-非市区的区别解释预测与应用关系的假设。此外，回归在教育水平相关性、手术紧急程度和手术定价方面也都有相应的发现。

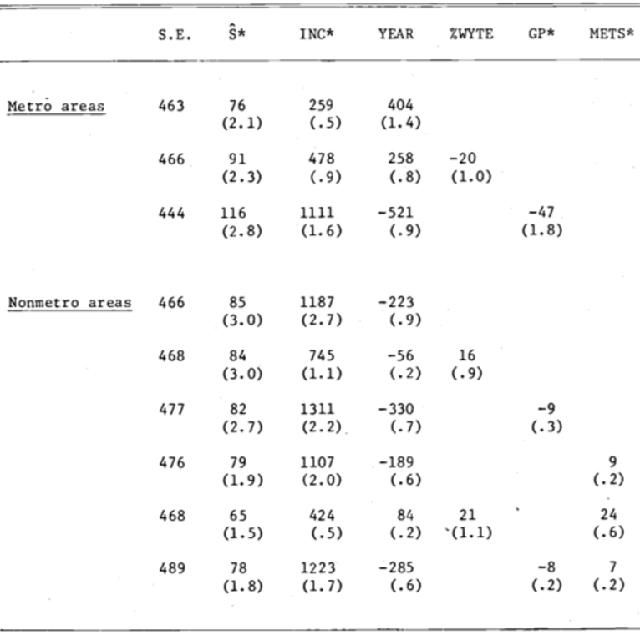
研究结论

1.预测的供给与需求在不同条件下均呈正相关。

2.供给与需求的这种影响在1970年和1963年都是有效的，尽管数量测量对于大量抽样误差具有主观性且不同年份之间的数据相关性不高。

3.无论是否将地区区分为市区和非市区，这种回归都是有效的。

4.供给在需求上的影响与人们教育水平是呈负相关性的。

5.供给的影响对于非紧急和非必须的外科手术及医生的影响是更加强烈的。

6.供给与手术定价成正相关。

本文转载自其他网站，不代表健康界观点和立场。如有内容和图片的著作权异议，请及时联系我们（邮箱：guikequan@hmkx.cn）

文章来源：《健康必读》 网址: http://www.jkbdzzs.cn/zonghexinwen/2020/0514/400.html